MazeGroup Research Institute/Maths/Fonctions

Niveau du cours : 3ème, Seconde

Une fonction en mathématiques est une expression à une ou plusieurs variables (inconnus), elle ne retourne de cette expression qu'une seule valeur.

Ainsi, $f(x)=x+1$ est une fonction qui prend la variable $x$ en entrée et retourne le résultat de l'expression $x+1$ en sortie. On peut donc l'utiliser dans n'importe quelle expression, comme $4\times f(5)$ qui est égale à $24$ dans notre cas.

Image et antécédent

Toujours avec la même fonction, l'expression $f(2)$ est égale à $3$, on dit que $2$ est un antécédent de $3$ par la fonction $f$ et aussi que $3$ est l'image de $2$ par la fonction $f$. Une image peut avoir plusieurs antécédents mais un antécédent ne peut avoir qu'une seule image.

Représentation par un tableau

Si $f(x)=2x$, voici l’intervalle $[-2;4]$ :

$x$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$
$f(x)$	$-4$	$-2$	$0$	$2$	$4$	$6$	$8$

Représentation graphique

Si $f(x)={\frac {-x^{2}}{2}}$, voici l'intervalle $[-10;10]$ :

Fonctions linéaires

Une fonction est linéaire uniquement si elle est proportionnelle et que la droite qui est formée par celle-ci passe par l'origine.

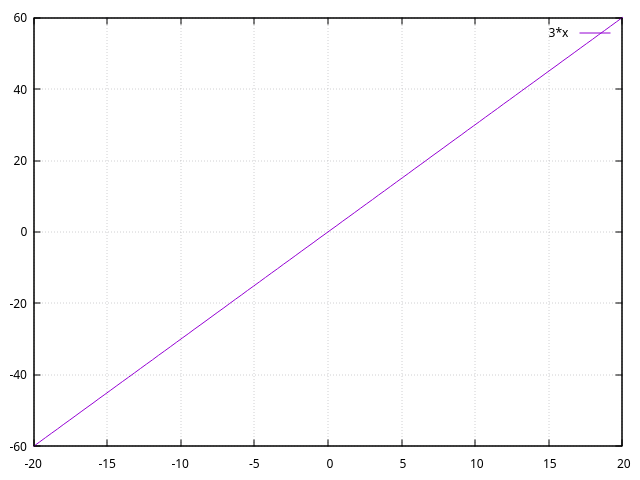
Si $f(x)=3x$, voici l'intervalle $[-20;20]$ :

---

Soit $a$ un nombre fixé.

En associant à chaque nombre « $x$ » un nombre « $ax$ » appelé image de $x$, on définit une fonction linéaire de coefficient $a$.

On notera cette fonction $f(x)=ax$

L’image de $x$ sera notée $f(x)$.

Fonctions affines

Une fonction est affine si elle retourne la somme d'un nombre et le produit de deux variables dont l'une est l'antécédent de la fonction.

Ainsi, $f(x)=4+3x$ est une fonction affine, elle respecte la forme $f(x)=ax+b$ dont les paramètres $a$ et $b$ ne dépendent pas de $x$.

Si $f(x)=4+3x$, voici l'intervalle $[-20;20]$ :

Note : la droite ne passe pas par l'origine, sinon ce serait une fonction linéaire.

Voir aussi

Articles connexes

• Fonction (mathématiques) - Wikipédia français

---

Cours par Genius_um. Avez-vous trouvé ce cours utile ou intéressent ? Notez le :

0.00

(un vote)

Des questions ?

Vous pourrez poser vos questions sur la page de discussion.

Commentaires

Loading comments...